The Simplest Quadratic The simplest Quadratic Equation isPlugging these values into the general form f(x) = a f b(x − h) k where f(x) = , we get f(x) = 4 3 This can be simplified to f(x) = 3 _____ The mapping rule is useful when graphing functions with transformations Any point (x, y) of a parent function becomes ( h, ay k)C) f(x) = 2(x 3) 2 = 2(x 3)) 2 0 a = 2 , h = 3 and k = 0 The vertex is at (3,0) and it is a minimum point since a is positive Interactive Tutorial Use the html 5 (better viewed using chrome, firefox, IE 9 or above) applet below to explore the graph of a quadratic function in vertex form f(x)=a (xh) 2 k where the coefficients a, h

3 Ways To Find The Maximum Or Minimum Value Of A Quadratic Function Easily
F(x)=a(x-h)^2+k form
F(x)=a(x-h)^2+k form-We want to put it into vertex form y=a(xh) 2 k;X = h 1h, k2 g1x2= a1x h22 k f1x2= ax2 g(x)=a(xh)2k If h > 0, the graph of f(x) = ax2 is shifted h units to the right If k > 0, the graph of y = a(x − h)2 is shifted k units up k f1x2= ax2 f1x2= ax2 h g1x2= a1x h22 k Transformations of f1x2= ax2 The Standard Form of a Quadratic Function The quadratic function
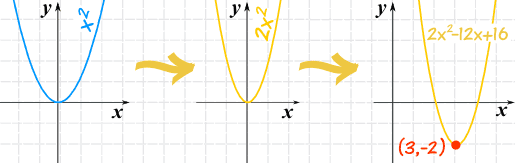



Graphing Quadratic Equations
A quadratic function is a function of degree two The graph of a quadratic function is a parabola The general form of a quadratic function is f(x) = ax2 bx c where a, b, and c are real numbers and a ≠ 0 The standard form of a quadratic function is f(x) = a(x − h)2 k36 is the value for 'c' that we found to make the right hand side a perfect square trinomialThe quadratic function f(x) = a(x − h)2 k is in standard form (a) The graph of f is a parabola with vertex (x, y) = (b) If a > 0, the graph of f opens In this case f(h) = k is the value of f (c) If a < 0, the graph of f opens In this case f(h) = k is the value of f please show step by step
Our equation is in standard form to begin with y=ax 2 bxc;Write the quadratic function in the formHow to Complete the Square In a regular algebra class, completing the square is a very useful tool or method to convert the quadratic equation of the form y = a{x^2} bx c also known as the "standard form", into the form y = a{(x h)^2} k which is known as the vertex form
color(red)( f(x) = (x1)^24) The vertex form of a quadratic is given by y = a(x – h)^2 k, where (h, k) is the vertex The "a" in the vertex form is the same "a" as in y = ax^2 bx c Your equation is f(x) = x^22x3 We convert to the "vertex form" by completing the square Step 1 Move the constant to the other side f(x)3 = x^22x Step 2Precalculus (7th Edition) Edit edition Solutions for Chapter 31 Problem 2E The quadratic function f (x) = a (x−h)2 k is in standard form (a) The graph of f is a parabola with vertex (____, ____) (b) If a > 0, the graph of f opens ________ In this case f (h) = k is the _______ value of f (c) If a f opensThe standard form of a quadratic function presents the function in the form latexf\left(x\right)=a{\left(xh\right)}^{2}k/latex where latex\left(h,\text{ }k\right)/latex is the vertex Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function The standard form is useful for determining




Graphing Quadratic Equations




The Vertex Of The Parabola Is At H K Ppt Video Online Download
Vertex of a Parabola Let us consider the general form of a quadratic function, {eq}f(x)=ax^2bxc {/eq} The graph of this function is a parabola that branches towards the positive ys for {eq}a>02 x 1 = f(x 2) f(x 1) x 2 x 1 (61) It's a linear approximation of the behavior of f between the points x 1 and x 2 7 Quadratic Functions The quadratic function (aka the parabola function or the square function) f(x) = ax2 bx c (71) can always be written in the form f(x) = a(x h)2 k (72) where V = (h;k) is the coordinate of the vertexMeanvalue forms of the remainder — Let f R → R be k 1 times differentiable on the open interval with f (k1) continuous on the closed interval between a and x Then = () ()!() for some real number ξ L between a and xThis is the Lagrange form of the remainder Similarly, = () ()!() ()for some real number ξ C between a and xThis is the Cauchy form of the remainder



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora




Quadratic Functions
Express f ( x) in the form a ( x − h) 2 k f (x) = −4x 2 24x − 17 Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThe basic or general form of a quadratic function is shown below, where A, B and C are fixed, numerical constants, and where B or C can be zero If A = 0, of course, there is no x 2 term and it's not a quadratic Terms with x to the first and zero powers are shown, but in practice we write x 1 = x and x 0 = 1 (which is not written at all the ghost 1) The form is usually written like this,




Quadratic Functions




The Following Graph Of F X X2 Has Been Shifted Into The Form F X X H 2 K What Is The Brainly Com
The equation y = 3x 2 12x 11 Vertex form of a parabola is y = a (x h ) 2 k Here x 2 coefficient is 3, for perfect square make x 2 coefficient 1 by dividing each side by 3 y = 3x 2 12x 11 y /3 = x 2 4x 11/3 To change the expression into a perfect square trinomial add (half the x coefficient)² to each side of the expressionAvertex form f(x) = 10(x 4)2 5 standard form f(x) = −10x2 40x 165 bvertex form f(x) = −6(x − 4)2 3 standard form f(x) = −6x2 7x − 24The Graph of Quadratic Function Thank you so much for joining our Grade 9 First Quarter Math Tutorials Keep on Sharing and enjoy learning




Answered Create A New Function In The Form Y Bartleby
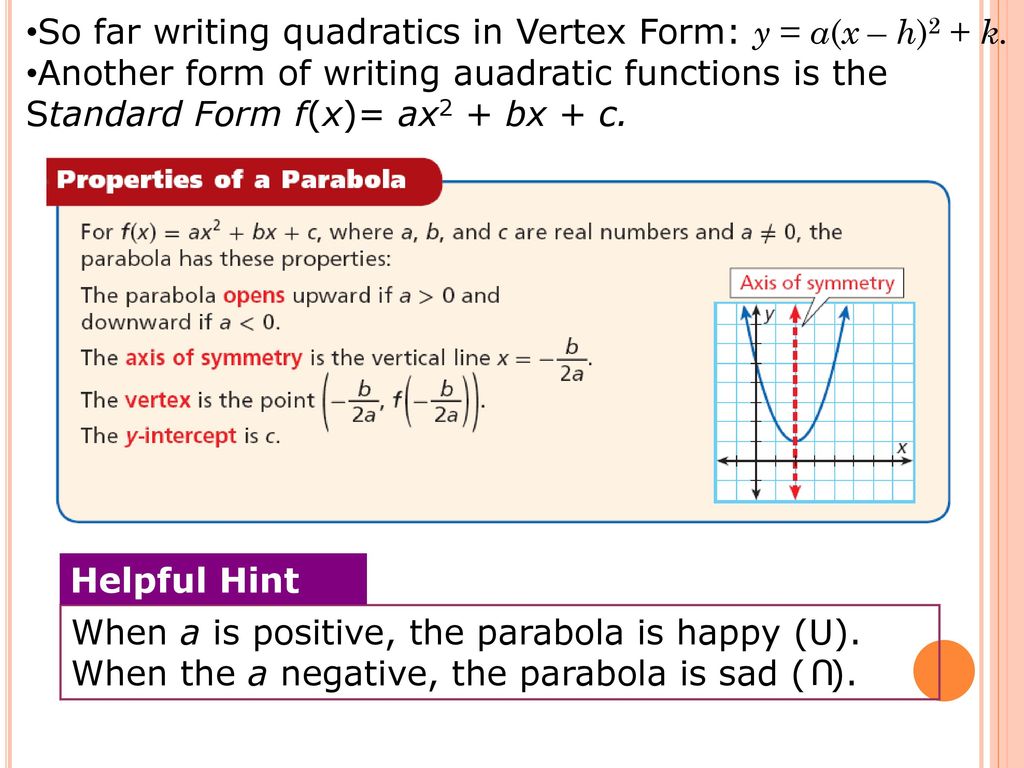



5 2 Properties Of Quadratic Functions In Standard Form Ppt Download
To Convert from f (x) = ax2 bx c Form to Vertex Form Method 1 Completing the Square To convert a quadratic from y = ax2 bx c form to vertex form, y = a ( x h) 2 k, you use the process of completing the square Let's see an example Convert y = 2x2 4x 5 into vertex form, and state the vertex Equation in y = ax2 bx c formGraphing f (x) = a(x − h)2 k CCore ore CConceptoncept Graphing f (x) = a(x − h)2 k The vertex form of a quadratic function is f (x) = a(x − h)2 k, where a ≠ 0 The graph of f (x) = a(x − h)2 k is a translation h units horizontally and k units vertically of the graph of f (x) = ax2 The vertex of the graph of f (x) = a(x − hF(x) = a(b)xh k Describe the transformations of each variable in the table Variable Effect on the Graph of the Line k* When "k" is positive equation for the line of an asymptote for a function in the form of f(x) = abx is always y = _____ Identify the asymptote and yint of each graph a



Solved The Graph Shows G X Which Is A Translation Of F X X 2 Write The Function Rule For G X Write The Answer In The Form A X H 2 K Course Hero
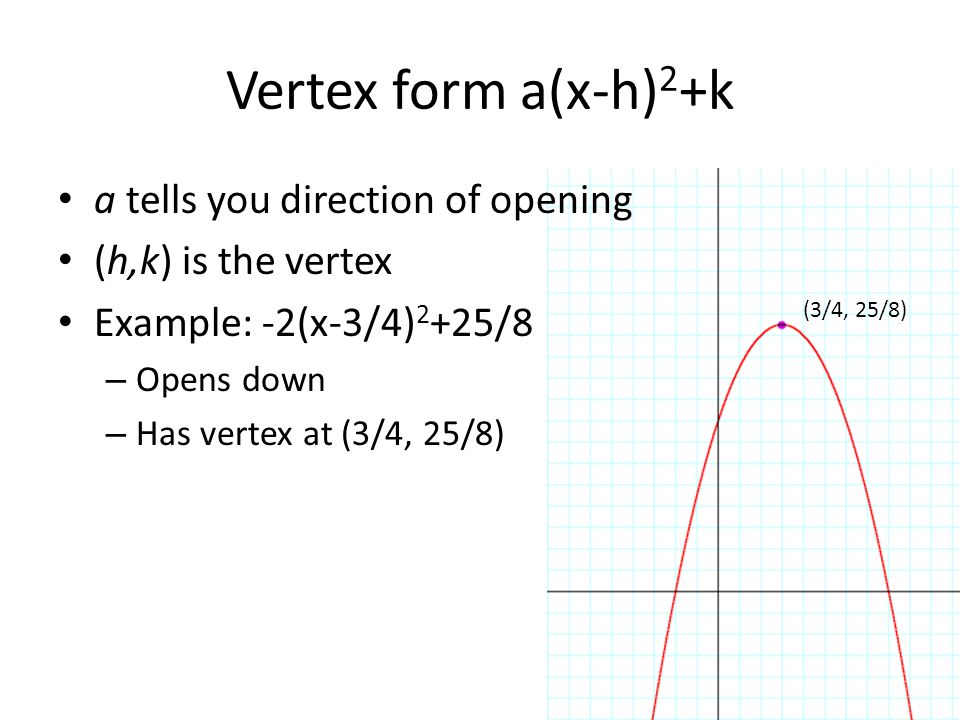



Vertex Form Ppt Download
Rearrange f (x) = x2 6x 12 into this form using the method of completing the square f (x) = (x2 6x9)−9 12 f (x) = (x 3)2 3 ← in vertex form Answer link Alan P f (x) = (x 3)2 3 (with some simplification, see below)LESSON 2 Graphing Quadratic Functions in Standard Form f(x)=ax^2bxcLESSON 3 Graphing Quadratic Functions in Vertex Form f(x)=a(xh)^2 kLESSON 4 Graphing Quadratic Functions in Intercept Form f(x)= a(xp)(xq)LESSON 5 Comparing and Graphing Quadratic Functions in Different Forms LESSON 6 Completing the Square of a Quadratic FunctionVertex form of a quadratic equation is y=a(xh) 2 k, where (h,k) is the vertex of the parabola;




Quick Review Before Hw Quiz Y A X H 2 K Form Vertex H K Axis X H Up If A 0 Down If A 0 Ex Y X 1 2 4 Y 1 X 1 2 4 A 1




Standard Form To Vertex Form Without Completing The Square Method Algebra 2 Youtube
The vertex form of a parabola is another form of the quadratic function f(x) = ax 2 bx c The vertex form of a parabola is f(x) = a(x h) 2 k The a in the vertex form of a parabola corresponds to the a in standard form If a is positive, the parabola will open upwards If a is negative, the parabola will open downwardsAnswer to Write the quadratic function in the form f(x)= a(x h)^2 k Then, give the vertex of its graph f(x)= 2x^2 4x 4 By signing up, What is the vertex form, f(x) = a(x − h)2 k, for a parabola that passes through the point (4, −3) and has (5, 2) as its vertex What is the standard form
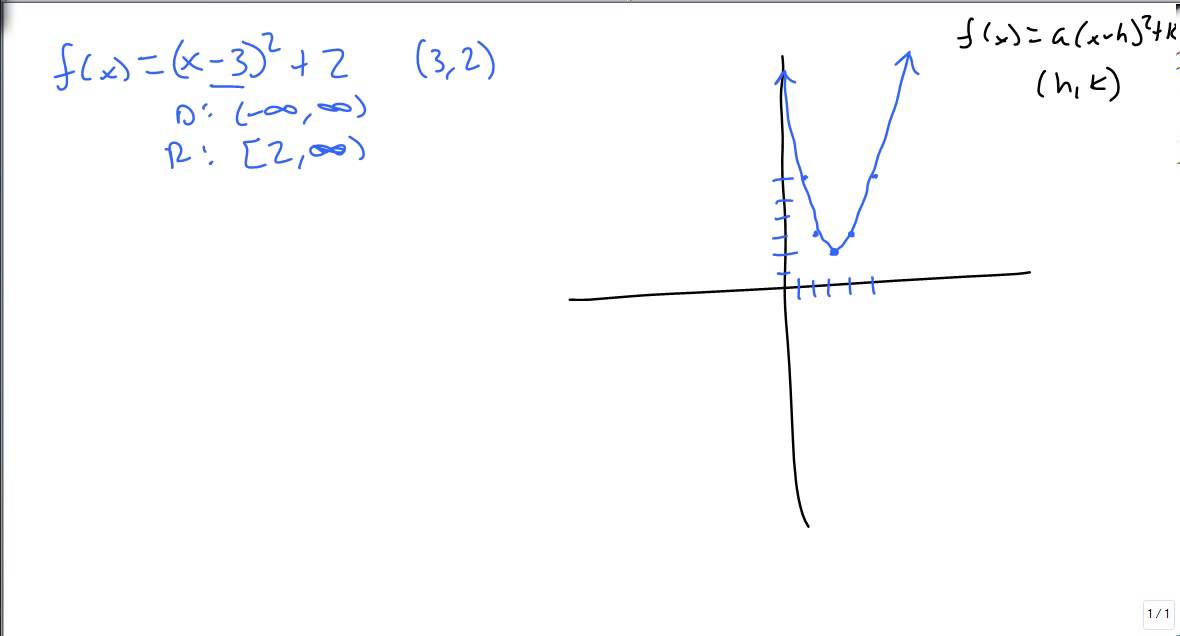



Graph By Transformations F X A X H 2 K Youtube



In Vertex Form Y A X H 2 K Which Letter Indicates A Stretch Change In Width Quora
Question Write the quadratic function in the form f(x)=a(xh)^2k Then, give the vertex of its graph f(x)=−2x^212x any help greatly appreciated Answer by lwsshak3() (Show Source) You can put this solution on YOUR website!Learn how to graph a parabola in the form y=(xh)^2k!Make sure to like this video if you found it helpful and feel free to leave feedback in the comments seA vertical stretch or compression a > 0, the parabola opens up and there is a minimum value a< 0, the parabola opens down and there is a maximum value (may also be referred to as a reflection in the xaxis) 1




Write The Quadratic Function In The Form G X Chegg Com



2
Complete the square to write the function in f(x) = a(x − h)2 k form Determine the vertex and the axis of symmetry of the graph of the functionThat would give us X squared minus six X And then I'm gonna put the minus 11 in the back So we need to complete the square by adding something here What is the vertex form, f(x) = a(x − h)2 k, for a parabola that passes through the point (1, −7) and has (2, 3) as its vertex what is the standard form of the equation?
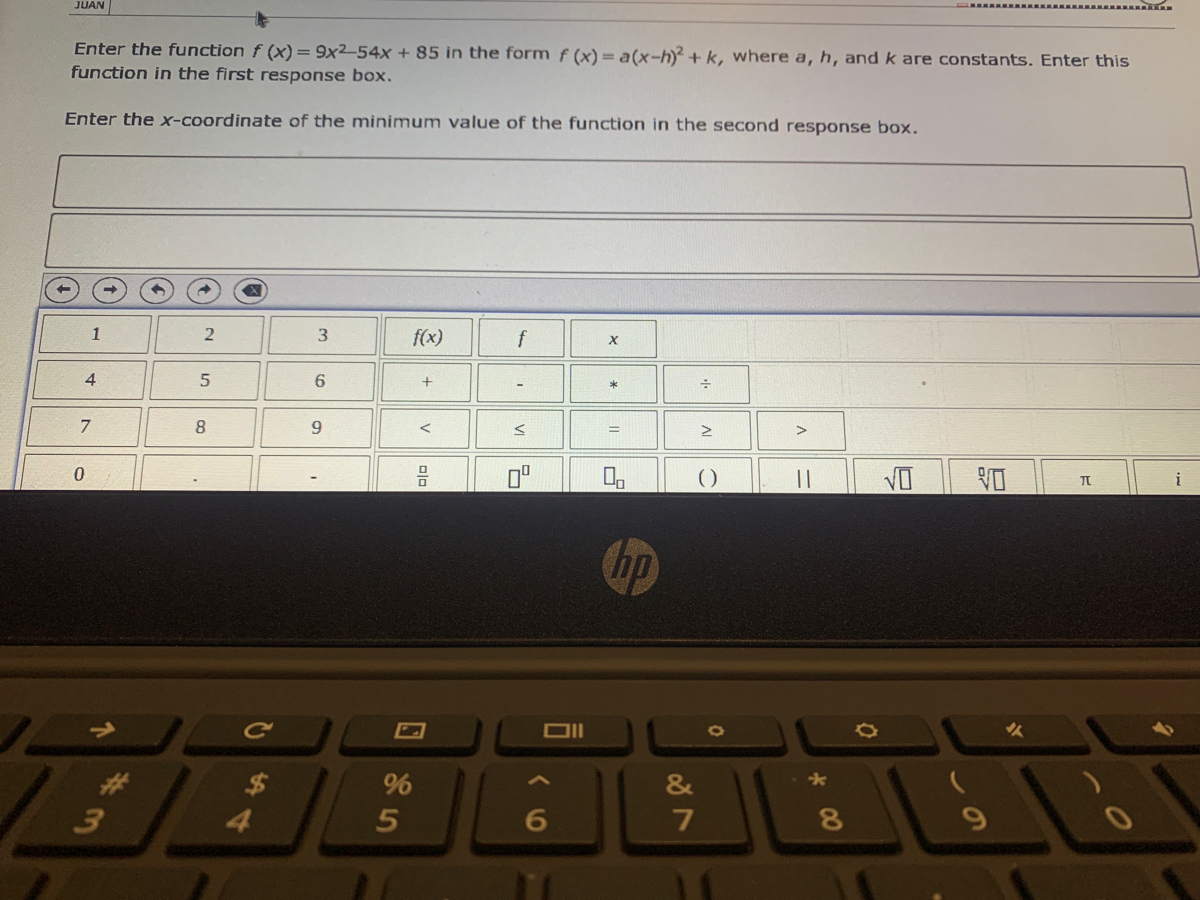



Answered Enter The Function F X 9x2 54x 85 Bartleby




The Following Graph Of F X X2 Has Been Shifted Into The Form F X X H 2 K Brainly Com
A quadratic function in the form f(x) = a(x h)2 k, where a 6= 0, is said to be in standard form The vertex of the parabola is located at (h;k) The graph of a quadratic function is a parabola If a > 0, the parabola opens up k is the minimum functional value, it occurs when x = hThe vertex will be the values for (h, k) and the given point will be the values for the point (x, f(x)) f(x) = a(x h) 2 2 = a Now, we can substitute the value for "a" and the vertex into our standard form equation f(x) = a(x h) 2 k f(x) = 2(x 1) 2 (3) f(x) = 2(x 1) 2 3 standard form To get the general form equation weWith a couple of substitutions, this can be written in the new standard form f(x) = a ( x h ) 2 k where h = b/(2a) and k = (4ac b 2) / (4a) Do not worry about what k is, but you might want to memorize the value for h The xcoordinate of the vertex is b/(2a) The ycoordinate is what you get when you plug b/(2a) back into the



1



Graphing Quadratic Functions
The graph of f is reflected in the line \(y = x\) to give the graph of g (i) Write down the yintercept of the graph of g (ii) Sketch the graph of g, noting clearly any asymptotes and the image of AConsider the graph of the parabola y=ax^2 Its vertex is clearly at (0,0) Now, if you replace x with xh in any equation, its graph gets shifted to the right by a distance of hWe can convert to vertex form by completing the square on the right hand side;




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21




The Graph Of F X X 2 Has Been Shifted Into The Form F X X H 2 K What Is The Value Of H A 1 B Brainly Com
Formula f(x) = a(x h) 2 k The Parabola always produces a "U"shaped graph which can open upwards or downwards depending on the value of "a" Given the values of a, h, and k, fill them into the formula to produce the equation of the graph() = is called the vertex form, where h and k are the x and y coordinates of the vertex, respectively The coefficient a is the same value in all three forms To convert the standard form to factored form , one needs only the quadratic formula to determine the two roots r 1 and r 2 Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open down




Explaining A And H When You Have Y A X H 2 Youtube




It S All In The Family Families Of Quadratic Functions
The standard form of a quadratic function is f(x)=a(xh) 2 k, where (h,k) is the vertex of the parabola The value of 'a' determines the direction of the graph of the parabola Sometimes, a quadratic function is not written in its standard form It is written as f(x) = ax 2 bx c and we may have to change it into the standard formSolve Step Graph f(x) = x 2 6x 8 Complete the square * f(x) = x 2 6x 99 8 Take half of 6 and square it f(x) = (x 3) 21 (x 3) 2 = x 2 6x 9Vertex (3,1) Vertex is (h,k)This means the vertex is shifted 3 units left and 1 unit down from the origin *Check out completing the square for help with this stepThe vertex of a parabola is the point at the top or bottom of the parabola 'h' is 6, the first coordinate in the vertex 'k' is 4, the second coordinate in the vertex 'x' is 2



In The Following Exercises Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown Bartleby
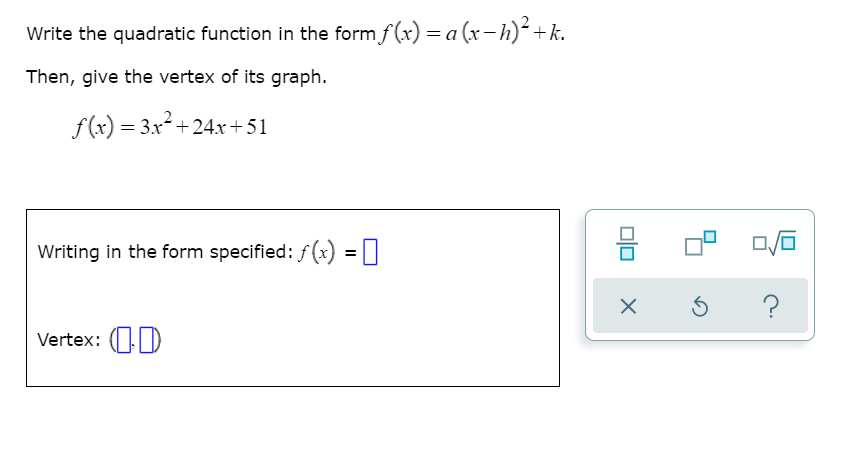



Answered Write The Quadratic Function In The Bartleby
Graph the function using transformations Graph a quadratic function in the vertex form f(x) = a(x − h)2 k using properties Rewrite the function in f(x) = a(x − h)2 k form Determine whether the parabola opens upward, a > 0, or downward, a < 0 Find the axis of symmetry, x = hA quadratic function f in vertex form is written as f(x) = a(x h) 2 k where h and k are the x and y coordinates respectively of the vertex (minimum or maximum) point of the graph The graph of of f is a parabola with the vertical line x = h as an axis of symmetry Find quadratic function knowing its vertex and a point Example 1Graphing Quadratic Equations A Quadratic Equation in Standard Form (a, b, and c can have any value, except that a can't be 0)Here is an example Graphing You can graph a Quadratic Equation using the Function Grapher, but to really understand what is going on, you can make the graph yourself Read On!




Algebra Ii 9 5a Graphs Of F X A X H K Guidelines For Graphing Quadratic Functions Youtube
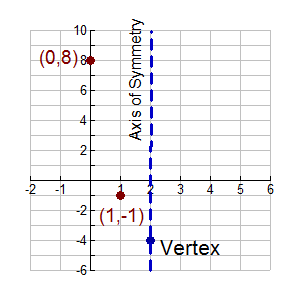



Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math
Simple and best practice solution for f(x)=a(xh)2k equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so




Graphing Parabolas
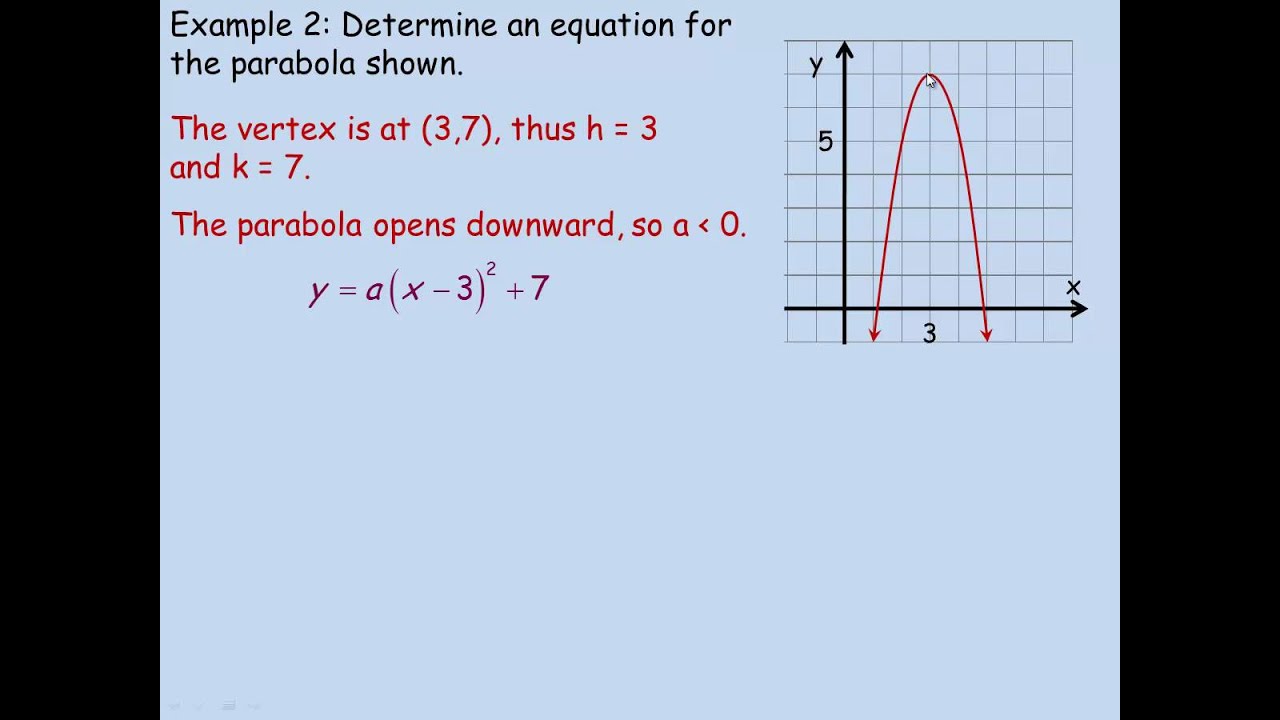



Graphing Y A X H K Youtube



Solved Use The Vertex H K And The Point On The Graph Xy To Find The Standard Form F X A X H 2 K Of This Equation Quadratic Function Course Hero




Quadratic Functions
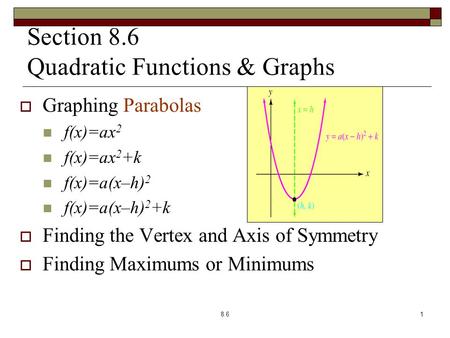



Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download




Mathematics Learners Material Module 2 Q



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions



Search Q Axis Of Symmetry Tbm Isch




3 Ways To Find The Maximum Or Minimum Value Of A Quadratic Function Easily
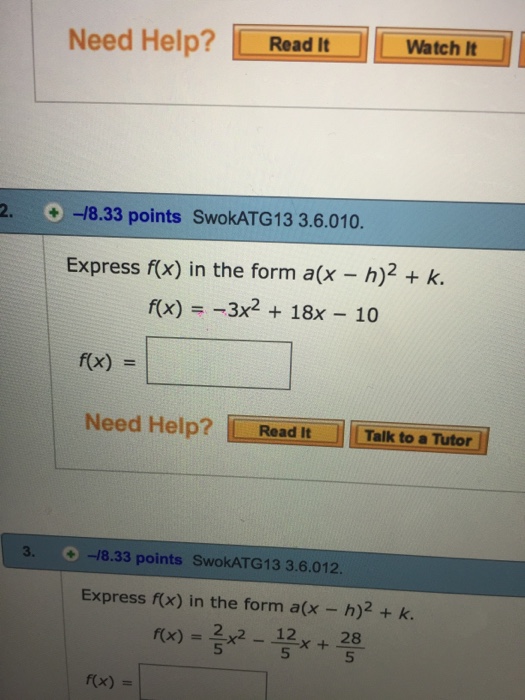



Express F X In The Form A X H 2 K F X Chegg Com




2 4 Quadratic Functions Ppt Download



Solution Write The Given Expression In The Form F X A X H 2 K Identify The Vertex F X 6 5x 10x 2



Quadratic Functions In The Form Y A X H 2 K Ppt Download




Rewrite The Following Quadratic Functions In Chegg Com




Changing A Quadratic Function Into Vertex Form Youtube




Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id
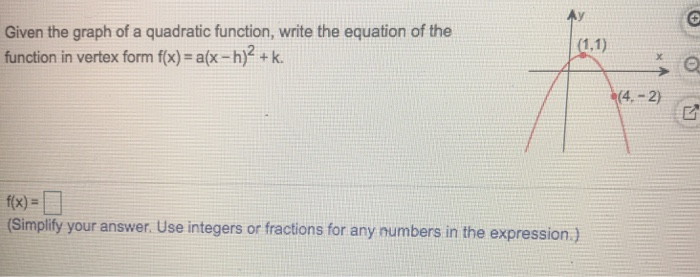



Given The Graph Of A Quadratic Function Write The Chegg Com
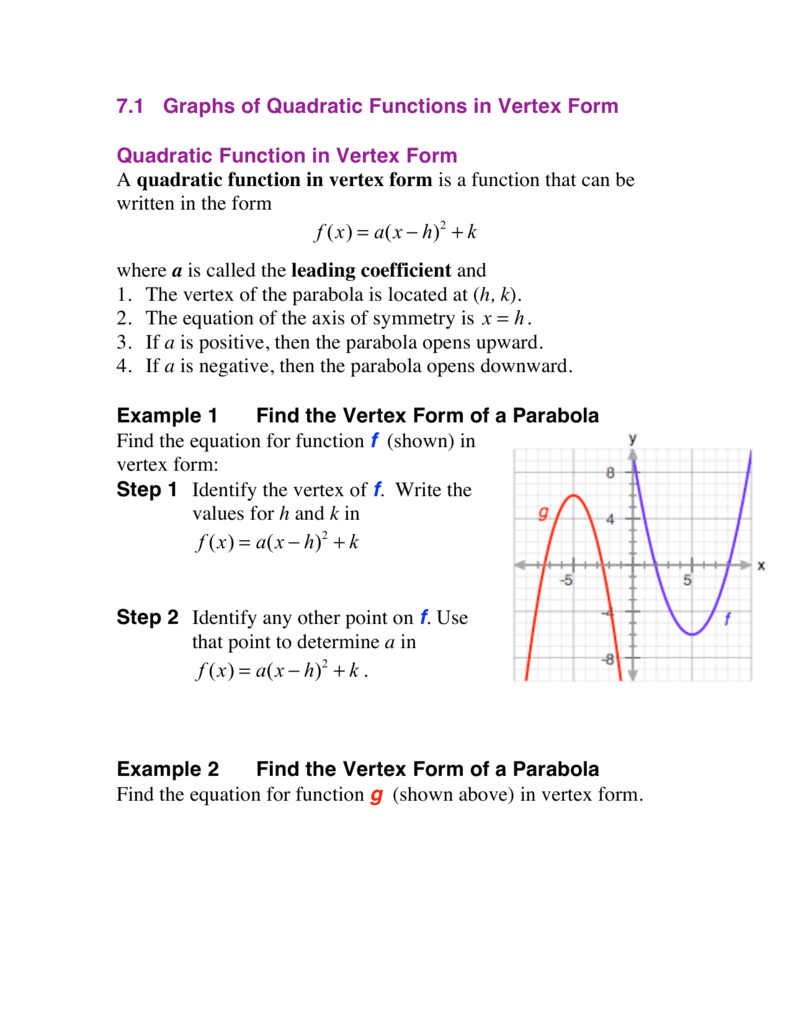



F X A X H 2 K F X A X H 2 K F X A X H 2 K




Write The Quadratic Function In The Form Chegg Com
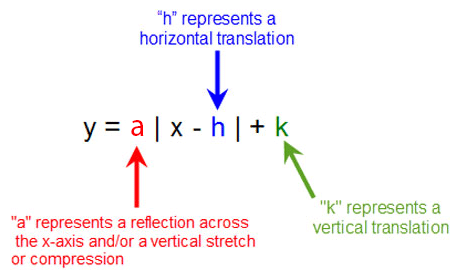



Untitled Document




Quadratic Function Formulas Definition Graphs Examples




Vertex Form Introduction Video Khan Academy



In The Following Exercises Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown Bartleby




Section 5 3 Transforming Parabolas Standard Form Vs Vertex Form Standard Form Is Y Ax 2 Bx C Vertex Form Is Y A X H 2 K Ppt Download




Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown F X Brainly Com




Calgebra A1 8 4 Graphing F X A X H 2 K Youtube
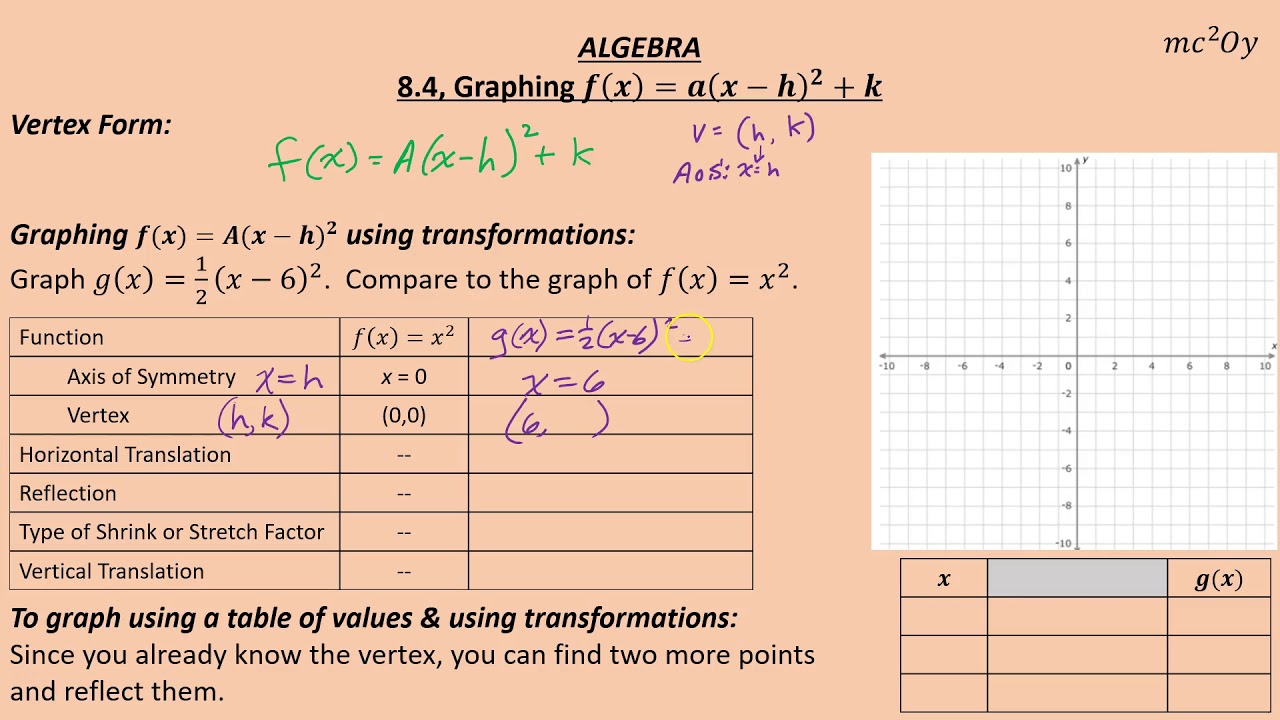



A 8 4 Graphing F X A X H 2 K Youtube




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube




How To Graph A Quadratic Equation 10 Steps With Pictures




Quadratic Functions



Solution Write The Quadratic Function In The Form F X A X H 2 K Find The Vertex And Graph The Function A F X X 2 6x B F X X 2 4x 1 C F X 3x 2 10x 2




The Vertex Form Of A Quadratic Function Is F X A X H 2 K What Is The Vertex Of Each Function Brainly Com
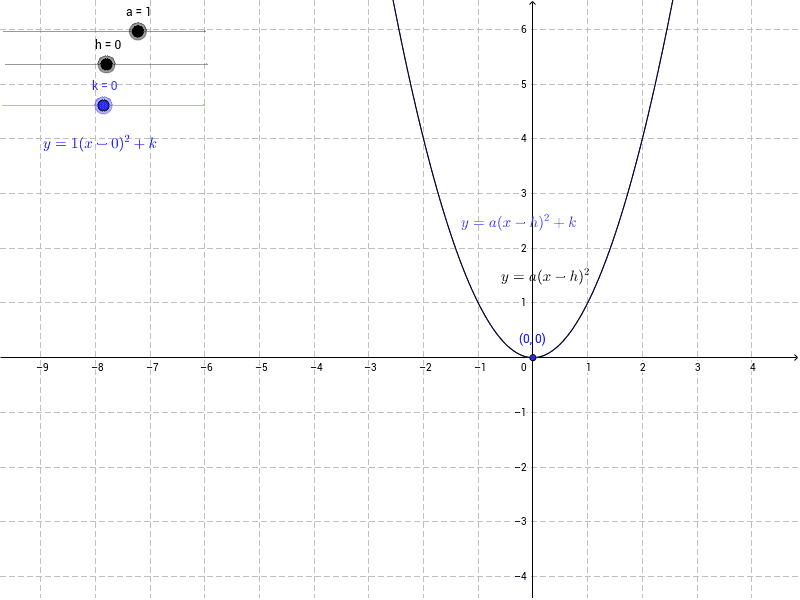



Investigating The Graph Of Y X H 2 K Geogebra



2




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube




Quadratic Function Wikipedia
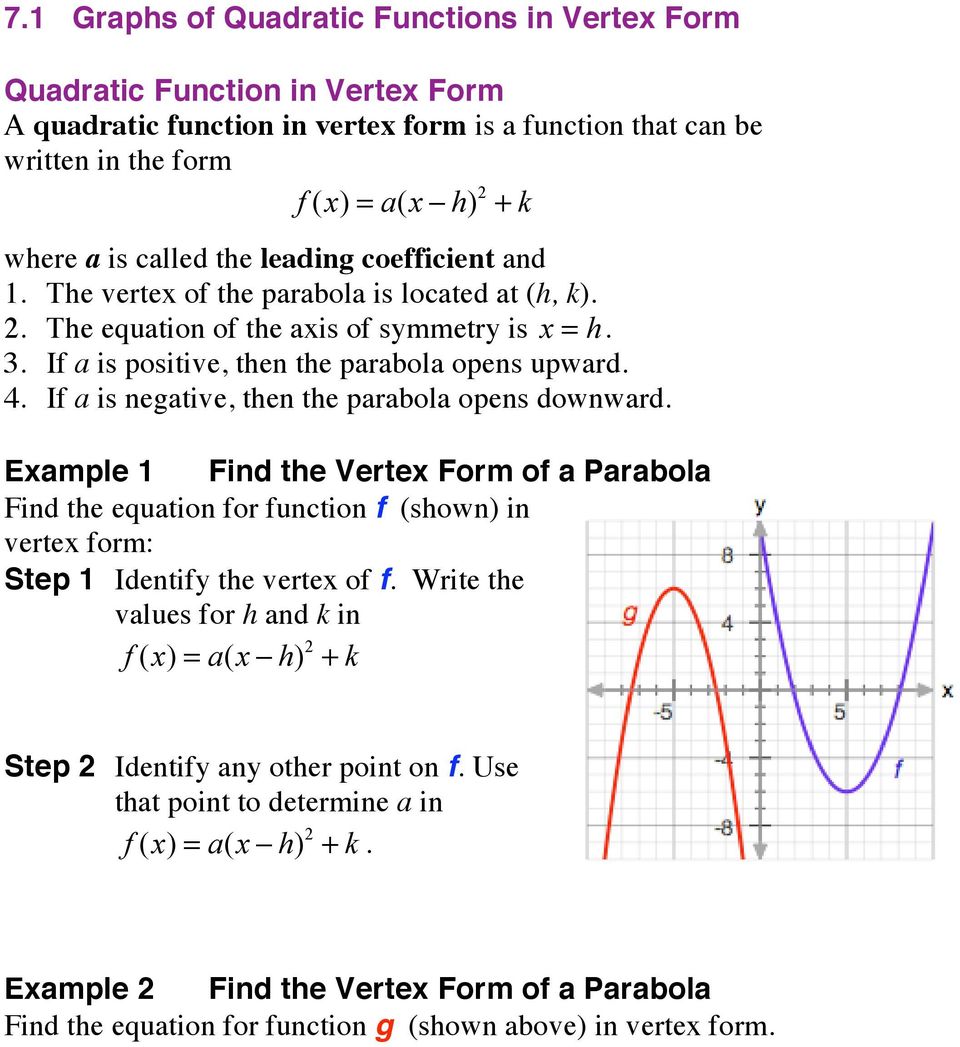



7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download




A Lesson On The Behavior Of The Graphs Of Quadratic Functions In The Form Y A X H 2 K Ppt Download




Quadratic Function Wikipedia



In The Following Exercises Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown Bartleby



2




Also Identify The Vertex No Need To Sketch Write The Quadratic Function In A X H 2 K Form Hint Homeworklib




Graphing Quadratics Vertex Form Algebra Video Khan Academy



Illustrative Mathematics




Finding Features Of Quadratic Functions Video Khan Academy



Illustrative Mathematics




How To Graph A Quadratic Equation 10 Steps With Pictures




Graphing Parabolas
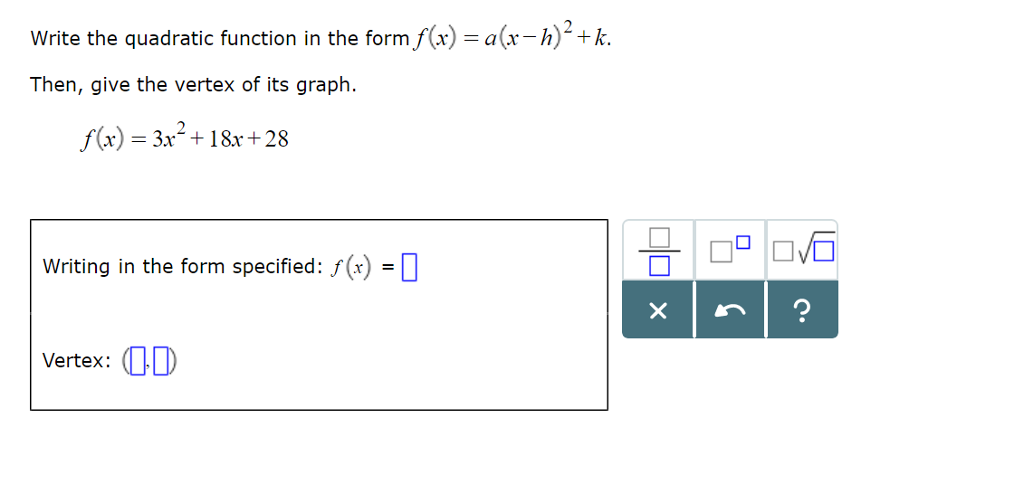



Write The Quadratic Function In The Form F X Chegg Com
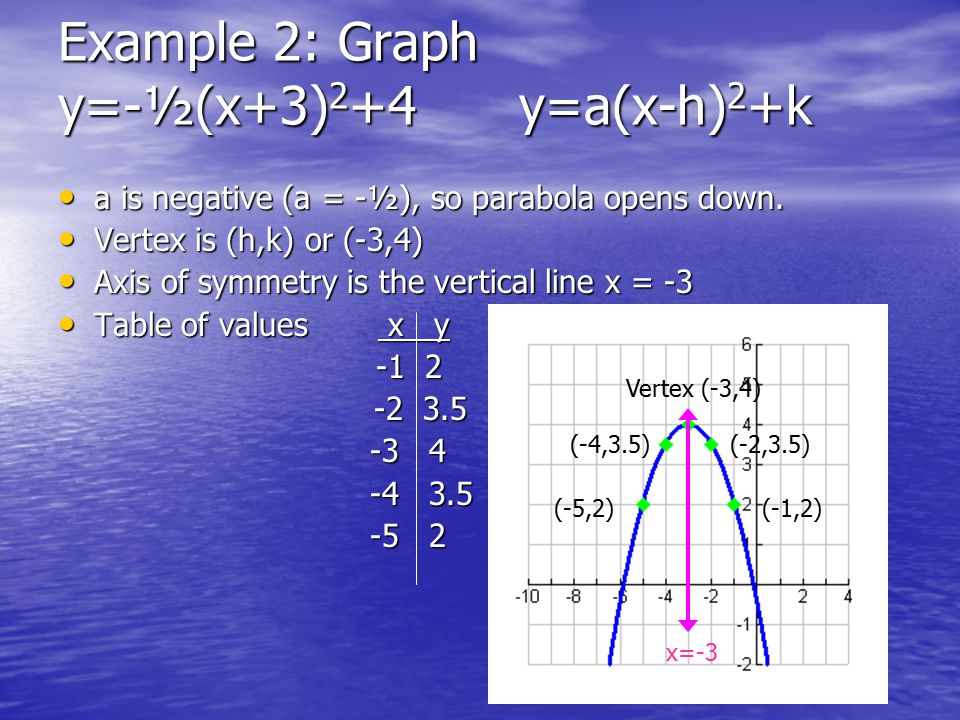



1 2 Graphing Quadratic Functions In Vertex Or Intercept Form Ppt Video Online Download




Write The Quadratic Function In The Form F X Chegg Com




Transform The Following Quadratic Function Into The Vertex Form F X A X H 2 K And Identify The Brainly Ph




Vce Mathematical Methods Units 1 And 2 4g Graphing Quadratic Functions




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21



Vertex Form Calculator



Search Q Standard Form Tbm Isch




Modeling Quadratic Change Flashcards Quizlet
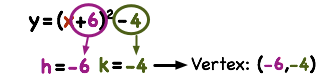



How Do You Convert A Quadratic From Standard Form To Vertex Form By Completing The Square Printable Summary Virtual Nerd



Illustrative Mathematics



Quadratic Function
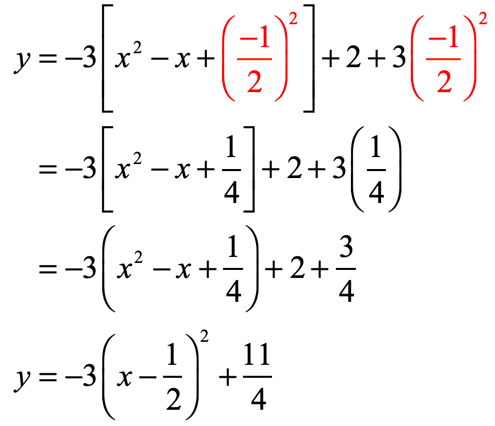



Completing The Square Step By Step Chilimath




Determine The Quadratic Function Of The Form F X Chegg Com



Math Spoken Here About Quadratics 3




Quadratic Functions




Unit 5 Quadratic Functions Flashcards Quizlet




How To Write Quadratic Functions Video Lesson Transcript Study Com




Quadratic Functions
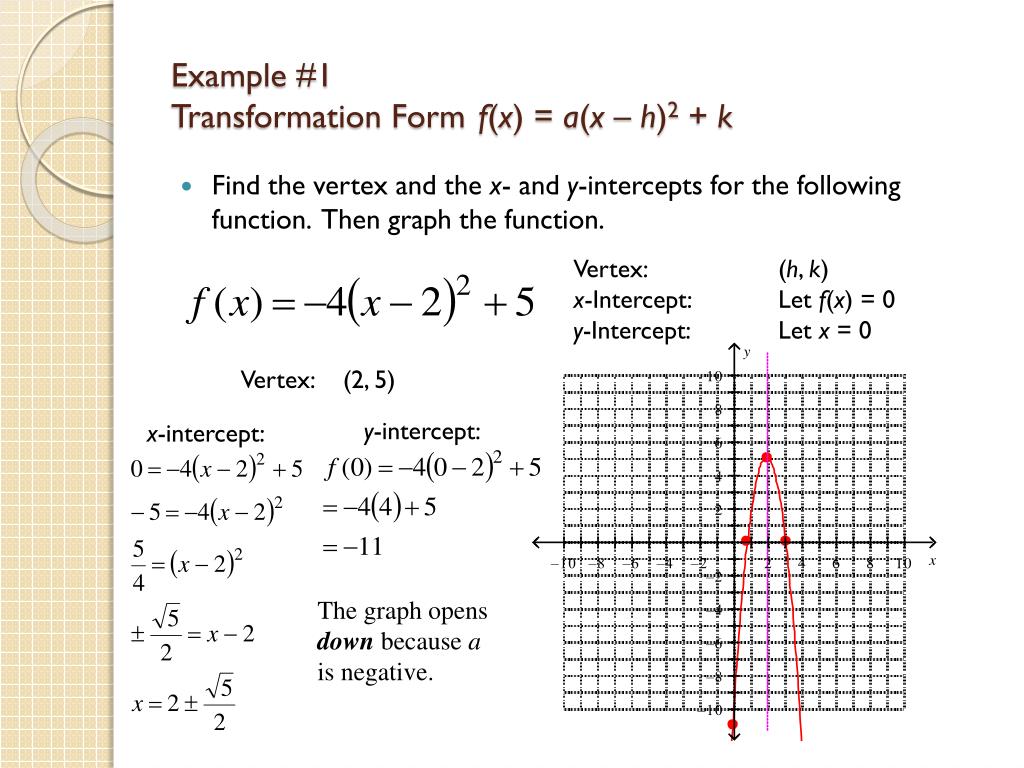



Ppt 3 3 Quadratic Functions Powerpoint Presentation Free Download Id




Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation
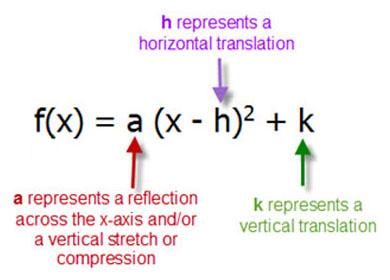



Untitled Document
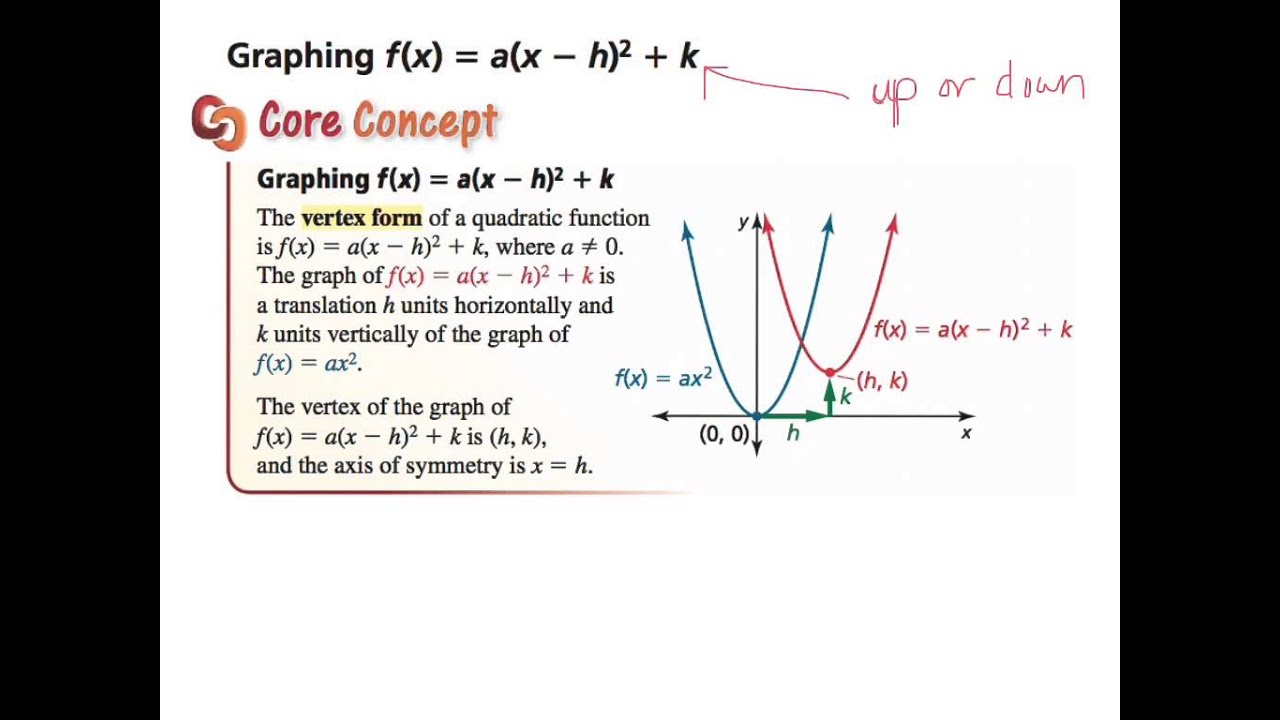



7th Section 8 4 Graphing F X A X H 2 K Youtube
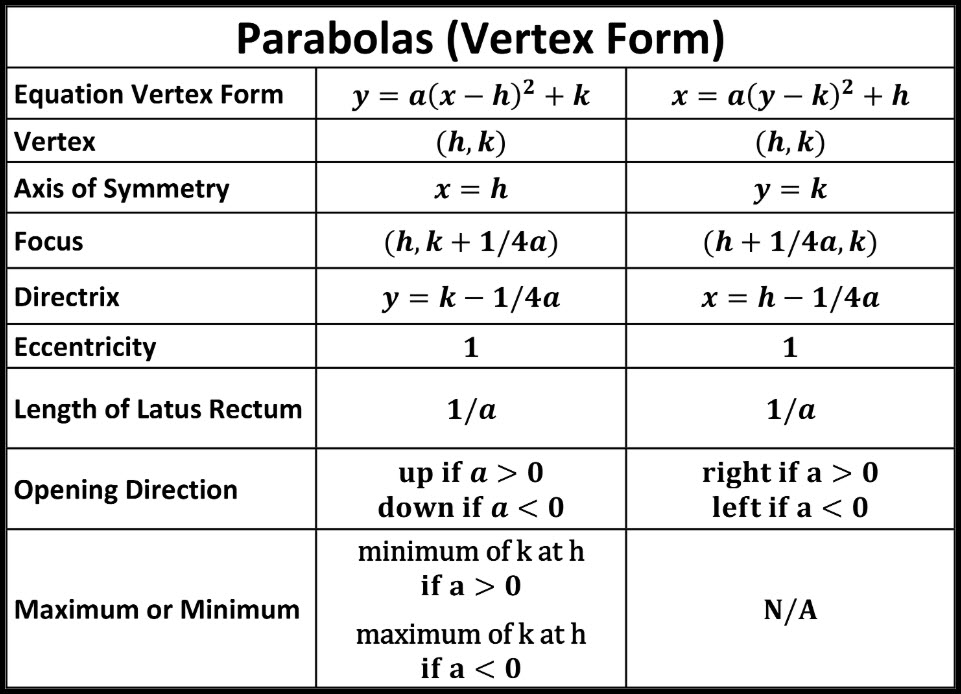



Parabolas Andymath Com




Ch 7 Tutoring Notes Quadratics




Graphing A Parabola In The Form Y X H 2 K Youtube




The Vertex Form Of A Quadratic Function Is F X A X H 2 K What Is The Vertex Of Each Function Brainly Com




Quadratic Functions Ppt Download



No comments:
Post a Comment